CURSO MÍDIAS NA EDUCAÇÃO

Este Blog, Fazer Matemático foi criado como um dos instrumento de avaliação, do Módulo 3,  do Curso Mídias na Educação, realizado pela Universidade Estadual do Sudoeste da Bahia - UESB, sob a orientação da tutora Corina Flores. Nele disponibilizo textos sobre Par Ordenado e Produto Cartesiano, todos apresentados de forma simples e descontraída, a fim de proporcionar as pessoas que o acessem uma melhor compreensão do conteúdo. Fazer Matemático é um Blog destinado a professores e alunos do Ensino Fundamental II e do Ensino Médio, enfim, ele é recomendado a todos que se interessem pela temática.

IMPORTÂNCIA DAS FUNÇÕES

A noção de Função foi-se construindo e aperfeiçoando ao longo de vários séculos. O estudo de função não é restrita apenas aos interesses da Matemática, as funções fazem parte do nosso cotidiano e estão presente na realização das coisas mais elementares que fazemos.
Nem sempre percebemos, mas estamos em contato com as funções a todo momento, por exemplo: quando assistimos ou lemos um jornal, muitas vezes nos deparamos com um gráfico, que nada mais é que uma relação, comparação de duas grandezas ou até mesmo uma função, mas representada graficamente. Para que esse gráfico tome forma é necessário que essa relação, comparação seja representada em uma função na forma algébrica.
Foi Dirichlet quem criou a definição "formal" de função moderna, para ele uma função é um caso especial de uma relação. Relação é um conjunto de pares ordenados, onde cada elemento do par pertence a um dos conjuntos relacionados. Nas relações não existem restrições quanto à lei de correspondência entre os elementos dos conjuntos, já para as funções é costume introduzir restrições.
A proposta de construir um Blog com esta temática passa pela necessidade do conhecimento de alguns conteúdos como Equação, Par Ordenado, Produto Cartesiano, Relações Binárias, dentre outros, para podermos ter uma melhor compreensão do conceito de função.

RELAÇÕES BINÁRIAS

Par Ordenado

Produto Cartesiano

Relações Binárias

PAR ORDENADO

CONCEITO

Intuitivamente, um par ordenado consiste de dois termos, digamos a e b, dos quais um, digamos a, é designado como primeiro termo e b como segundo termo. Um par ordenado com primeiro termo a e segundo termo b é representado explicitamente por (a, b).

DEFINIÇÃO

O par ordenado (a, b) foi definido como {{a}, {a, b}} por K. Kuratowski em 1921. Em 1914 Wiener deu uma definição, historicamente importante, para par ordenado definindo (a, b) como {{a, Ø }, {b, { Ø }}}.

ELEMENTOS DE UM PAR ORDENADO

Num par ordenado P = (x, y), x é chamado abscissa, primeiro elemento, primeira coordenada ou primeira projeção. Já y é chamado ordenada, segundo elemento, segunda coordenada ou segunda projeção.

IGUALDADE DE PARES ORDENADOS

Se x e y são pares ordenados (representados não explicitamente), a igualdade x = y significa por definição que a abscissa de x é igual a abscissa de y e que a ordenada de x é igual a ordenada de y.

De outro modo, (a, b) = (c, d) significa por definição que a = c e b = d.

REFERÊNCIA HISTÓRICA

Os nomes Plano Cartesiano e Produto Cartesiano são homenagens ao seu criador René Descartes (1596-1650), filósofo e matemático francês. O nome de Descartes em Latim, era Cartesius, daí vem o nome cartesiano.

RENÉ DESCARTES

René Descartes (La Haye en Touraine, 31 de Março de 1596 — Estocolmo, 11 de Fevereiro de 1650), também conhecido como Renatus Cartesius, foi filósofo, físico e matemático francês. Notabilizou-se sobretudo por seu trabalho revolucionário na filosofia e na ciência, mas também obteve reconhecimento matemático por sugerir a fusão da álgebra com a geometria - fato que gerou a geometria analítica e o sistema de coordenadas (o plano cartesiano que hoje leva o seu nome).

Descartes considerado um dos pensadores mais importantes e influentes da História do Pensamento Ocidental, obteve grande destaque nos ramos da Filosofia e da Física, sendo considerado peça fundamental na Revolução Científica, por várias vezes foi chamado de "pai da Matemática" moderna e "o fundador da "filosofia moderna".

O MÉTODO

Descartes estabeleceu um método universal, inspirado no rigor matemático e em suas "longas cadeias de razão".

1- A primeira regra é a evidência: não admitir "nenhuma coisa como verdadeira se não a reconheço evidentemente como tal". Em outras palavras, evitar toda "precipitação" e toda "prevenção" (preconceitos) e só ter por verdadeiro o que for claro e distinto, isto é, o que "eu não tenho a menor oportunidade de duvidar".

Por conseguinte, a evidência é o que salta aos olhos, é aquilo de que não posso duvidar, apesar de todos os meus esforços, é o que resiste a todos os assaltos da dúvida, apesar de todos os resíduos, o produto do espírito crítico. Não, como diz bem Jankélévitch, "uma evidência juvenil, mas quadragenária".

2 - A segunda, é a regra da análise: "dividir cada uma das dificuldades em tantas parcelas quantas forem possíveis".

3 - A terceira, é a regra da síntese: "concluir por ordem meus pensamentos, começando pelos objetos mais simples e mais fáceis de conhecer para, aos poucos, ascender, como que por meio de degraus, aos mais complexos".

4 - A última á a dos "desmembramentos tão complexos... a ponto de estar certo de nada ter omitido".

Se esse método tornou-se muito célebre, foi porque os séculos posteriores viram nele uma manifestação do livre exame e do racionalismo.

PLANO CARTESIANO ORTOGONAL

O plano cartesiano ortogonal é constituído por dois eixos x e y perpendiculares entre si que se cruzam na origem. O eixo horizontal é o eixo das abscissas (eixo OX) e o eixo vertical é o eixo das ordenadas (eixo OY). Associando a cada um dos eixos o conjunto de todos os números reais, obtém-se o plano cartesiano ortogonal.
O termo ortogonal refere-se ao perpendicularismo entre os eixos.

LOCALIZAÇÃO DE UM PONTO NO PLANO

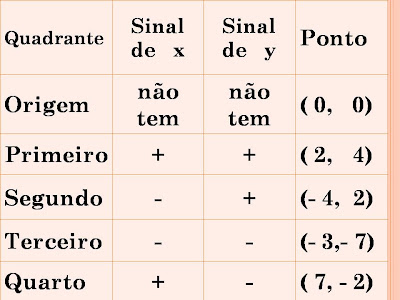
Os dois eixos dividem o plano em quatro regiões denominadas quadrantes sendo que tais eixos são retas concorrentes na origem do sistema formando um ângulo reto (90 graus). Os nomes dos quadrantes são indicados no sentido anti-horário.

Cada ponto P = (a, b) do plano cartesiano é formado por um par ordenado de números, indicados entre parênteses, a abscissa e a ordenada respectivamente. Este par ordenado representa as coordenadas de um ponto.


O primeiro número indica a medida do deslocamento a partir da origem para a direita (se positivo) ou para a esquerda (se negativo).


O segundo número indica o deslocamento a partir da origem para cima (se positivo) ou para baixo (se negativo).


Observe no desenho acima que: (a, b) ≠ (b, a) se a ≠ b.

QUADRANTES

Os nomes dos quadrantes são indicados no sentido anti-horário.

SINAL DAS COORDENADAS

Sinal das coordenadas de um ponto:

PRODUTO CARTESIANO

Definição:Dados dois conjuntos A e B, o produto cartesiano denotado por A x B (lê-se A cartesiano B) é o conjunto de todos os pares ordenados cujos primeiros elementos (primeiras coordenadas) pertencem a A e cujos segundos elementos (segundas coordenadas) pertencem a B.

A x B = { ( x, y ) / x A e y B }

EXEMPLO: PRODUTO CARTESIANO

Se A = {1, 2, 3} e B = {p, q} então:


A x B = {(1, p), (2, p), (3, p), (1, q), (2, q), (3, q)}


B x A = {(p, 1), (p, 2), (p, 3), (q, 1), (q, 2), (q, 3)}

Observe que:

A x B é diferente B x A.

CONSIDERAÇÕES SOBRE PRODUTO CARTESIANO

Observações:

1. Se A é não vazio e B é não vazio então:

A x B ≠ B x A

2. Se A = Ø ou B = Ø, por definição:

A x Ø = Ø x B = Ø

3. Se A possui m elementos e B possui p elementos, então:

n( A x B ) = n( A) x n( B )

n( A x B ) = m x p

4. A x A pode ser indicado por A2.

FRASES: RENÉ DESCARTES

FRASES RENÉ DESCARTES

Humanamente não existe um ser que seja feliz sem que o outro também seja.

Nada é mais justamente distribuído que o senso comum: ninguém pensa que precisa mais do que realmente já tenha.

"É propriamente não valer nada não ser útil a ninguém.""Não há nada que dominemos inteiramente a não ser os nossos pensamentos." “Não basta termos um bom espírito, o mais importante é aplicá-lo bem.”

Muitas vezes as coisas que me pareceram verdadeiras quando comecei a concebê-las tornaram-se falsas quando quis colocá-las sobre o papel.

René Descartes